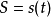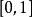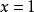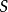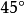內容簡介,一元微分,摺疊定義,摺疊幾何意義,積分相關,極限理論,常見符號,微積分歷史,積分學早期史,微積分產生,牛頓的發展,萊布尼茨,優先權之爭,第二次危機,創立意義,相關評價,套用及發展,近現代發展,前蘇聯,美國,中國,計算工具,
內容簡介
從廣義上說,數學分析包括微積分、函式論等許多分支學科,但是現在一般已習慣於把數學分析和微積分等同起來,數學分析成了微積分的同義詞,一提數學分析就知道是指微積分。
一元微分
摺疊定義
設函式
在某區間內有定義,
及
+ Δx在此區間內。如果函式的增量Δy = f(
+ Δx) – f(
)可表示為 Δy = AΔx + o(Δx)(其中A是不依賴於Δx的常數),而o(Δx)是比Δx高階的無窮小,那么稱函式f(x)在點
是可微的,且AΔx稱作函式在點x0相應於自變數增量Δx的微分,記作dy,即dy = AΔx。
通常把自變數x的增量 Δx稱為自變數的微分,記作dx,即dx = Δx。於是函式y = f(x)的微分又可記作dy = f'(x)dx。函式的微分與自變數的微分之商等於該函式的導數。因此,導數也叫做微商。
摺疊幾何意義
設Δx是曲線y = f(x)上的點M的在橫坐標上的增量,Δy是曲線在點M對應Δx在縱坐標上的增量,dy是曲線在點M的切線對應Δx在縱坐標上的增量。當|Δx|很小時,|Δy-dy|比|Δx|要小得多(高階無窮小),因此在點M附近,我們可以用切線段來近似代替曲線段。
積分相關
(1)定積分和不定積分
積分是微分的逆運算,即知道了函式的
導函式,反求原函式。在套用上,定積分作用不僅如此,它被大量套用於求和,通俗的說是求曲邊三角形的面積,這巧妙的求解方法是積分特殊的性質決定的。
一個函式的不定積分(亦稱原函式)指另一族函式,這一族函式的導函式恰為前一函式。
一個實變函式在區間[a,b]上的定積分,是一個實數。它等於該函式的一個原函式在b的值減去在a的值。
定積分和不定積分的定義迥然不同,定積分是求圖形的面積,即是求微元元素的累加和,而不定積分則是求其原函式,而牛頓和萊布尼茨則使兩者產生了緊密的聯繫(詳見
牛頓-萊布尼茨公式)。
含自變數、未知函式和它的微商(或偏微商)的方程稱為常(或偏)微分方程。未知函式為一元函式的微分方程,稱為常微分方程。未知函式為多元函,從而出現多元函式的偏導數的方程,稱為偏微分方程。
極限理論
十七世紀以來,微積分的概念和技巧不斷擴展並被廣泛套用來解決天文學、物理學中的各種實際問題,取得了巨大的成就。但直到十九世紀以前,在微積分的發展過程中,其數學分析的嚴密性問題一直沒有得到解決。十八世紀中,包括牛頓和萊布尼茲在內的許多大數學家都覺察到這一問題並對這個問題作了努力,但都沒有成功地解決這個問題。
整個十八世紀,微積分的基礎是混亂和不清楚的,許多英國數學家也許是由於仍然為古希臘的幾何所束縛,因而懷疑微積分的全部工作。這個問題一直到十九世紀下半葉才由法國數學家柯西得到了完整的解決,
柯西極限存在準則使得微積分注入了嚴密性,這就是
極限理論的創立。極限理論的創立使得微積分從此建立在一個嚴密的分析基礎之上,它也為20世紀數學的發展奠定了基礎。
註:在中世紀(14—17世紀)歐洲數學大發展的時期,我國基本處於停滯狀態(明、清時期)。所以,我國的數學家與微積分無緣。
常見符號
微分符號,
,
等,系由萊布尼茨首先使用。其中的"
"源自拉丁語中“差”(Differentia)的第一個字母。積分符號“
”亦由萊布尼茨所創,它是拉丁語“總和”(Summa)的第一個字母s的伸長(和
有相同的意義), “
” 為圍道積分。
微積分歷史
從微積分成為一門學科來說,是在17世紀,但是
積分的思想早在古代就已經產生了。
積分學早期史
公元前7世紀,古希臘科學家、哲學家泰勒斯就對球的面積、體積、與長度等問題的研究就含有微積分思想。公元前3世紀,
古希臘的數學家、力學家
阿基米德(公元前287~前212)的著作《
圓的測量》和《
論球與圓柱》中就已含有積分學的萌芽,他在研究解決拋物線下的
弓形面積、球和
球冠面積、
螺線下的面積和旋轉
雙曲線所得的體積的問題中就隱含著近代積分的思想。
 圖1萊布尼茨
圖1萊布尼茨中國古代數學家也產生過積分學的萌芽思想,例如三國時期的劉徽,他對積分學的思想主要有兩點:割圓術及求體積問題的構想。
微積分產生
到了十七世紀,有許多科學問題需要解決,這些問題也就成了促使微積分產生的因素。歸結起來,大約有四種主要類型的問題:第一類是研究運動的時候直接出現的,也就是求即時速度的問題。第二類問題是求曲線的切線的問題。第三類問題是求函式的最大值和最小值問題。第四類問題是求曲線長、曲線圍成的面積、曲面圍成的體積、物體的重心、一個體積相當大的物體作用於另一物體上的引力。
 圖2 牛頓-萊布尼茨公式
圖2 牛頓-萊布尼茨公式數學首先從對運動(如天文、航海問題等)的研究中引出了一個基本概念,在那以後的二百年里,這個概念在幾乎所有的工作中占中心位置,這就是函式——或變數間關係——的概念。緊接著函式概念的採用,產生了微積分,它是繼
歐幾里得幾何之後,全部數學中的一個最大的創造。圍繞著解決上述四個核心的科學問題,微積分問題至少被十七世紀十幾個最大的數學家和幾十個小一些的數學家探索過。其創立者一般認為是
牛頓和
萊布尼茨。在此,我們主要來介紹這兩位大師的工作。
實際上,在牛頓和萊布尼茨作出他們的衝刺之前,微積分的大量知識已經積累起來了。十七世紀的許多著名的數學家、天文學家、物理學家都為解決上述幾類問題作了大量的研究工作,如法國的
費馬、
笛卡爾、羅伯瓦、
笛沙格;英國的
巴羅、瓦里士;德國的
克卜勒;義大利的
卡瓦列利等人都提出許多很有建樹的理論。為微積分的創立做出了貢獻。
例如費馬、巴羅、笛卡爾都對求曲線的切線以及曲線圍成的面積問題有過深入的研究,並且得到了一些結果,但是他們都沒有意識到它的重要性。在十七世紀的前三分之二,微積分的工作沉沒在細節里,作用不大的細微末節的推理使他們筋疲力盡了。只有少數幾個大數學家意識到了這個問題,如詹姆斯·格里高利說過:“數學的真正劃分不是分成幾何和算術,而是分成普遍的和特殊的”。而這普遍的東西是由兩個包羅萬象的思想家
牛頓和
萊布尼茨提供的。十七世紀下半葉,在前人工作的基礎上,英國大科學家牛頓和德國數學家萊布尼茨分別在自己的國度里獨自研究和完成了微積分的創立工作,雖然這只是十分初步的工作。他們的最大功績是把兩個貌似毫不相關的問題聯繫在一起,一個是切線問題(微分學的中心問題),一個是求積問題(積分學的中心問題)。
牛頓和萊布尼茨建立微積分的出發點是直觀的無窮小量,因此這門學科早期也稱為無窮小分析,這正是現時數學中分析學這一大分支名稱的來源。牛頓研究微積分著重於從
運動學來考慮,萊布尼茨卻是側重於幾何學來考慮的。
牛頓的發展
牛頓在1671年寫了《
流數術和
無窮級數》,這本書直到1736年才出版,它在這本書里指出,變數是由點、線、面的連續運動產生的,否定了以前自己認為的變數是無窮小元素的靜止集合。他把
連續變數叫做流動量,把這些流動量的
導數叫做流數。牛頓在流數術中所提出的中心問題是:已知連續運動的路徑,求給定時刻的速度(微分法);已知運動的速度求給定時間內經過的路程(積分法)。
萊布尼茨
德國的萊布尼茨(又譯“萊布尼茲”)是一個博才多學的學者,1684年,他發表了現在世界上認為是最早的微積分文獻,這篇文章有一個很長而且很古怪的名字《一種求極大極小和切線的新方法,它也適用於分式和無理量,以及這種新方法的奇妙類型的計算》。就是這樣一篇說理也頗含糊的文章,卻有劃時代的意義。它已含有現代的
微分符號和基本微分法則。
1686年,萊布尼茨發表了第一篇積分學的文獻。他是歷史上最偉大的符號學者之一,他所創設的微積分符號,遠遠優於
牛頓的符號,這對微積分的發展有極大的影響。現今我們使用的微積分通用符號就是當時萊布尼茨精心選用的。
優先權之爭
微積分是能套用於許多類函式的一種新的普遍的方法,這一發現必須歸功於牛頓和萊布尼茨兩人。經過他們的工作,微積分不再是古希臘幾何的附庸和延展,而是一門獨立的學科。
歷史上,關於微積分的成果歸屬和優先權問題,曾在數學界引起了一場長時間的大爭論。1687年以前,牛頓沒有發表過微積分方面的任何工作,雖然他從1665年到1687年把結果通知了他的朋友。特別地,1669年他把他的短文《分析學》術給了他的老師巴羅,後者把它送給了John Collins。萊布尼茨於1672年訪問巴黎,1673年訪問倫敦,並和一些與牛頓工作的人通信。然而,他直到1684年才發表微積分的著作。於是就發生萊布尼茨是否知道牛頓工作詳情的問題,他被指責為剽竊者。但是,在這兩個人死了很久以後,調查證明:雖然牛頓工作的大部分是在萊布尼茲之前做的,但是,萊布尼茲是微積分主要思想的獨立發明人。
這場爭吵的重要性不在於誰勝誰負的問題,而是使數學家分成兩派。一派是英國數學家,捍衛牛頓;另一派是歐洲大陸數學家,尤其是
伯努利兄弟,支持萊布尼茨,兩派相互對立甚至敵對。其結果是,使得英國和歐洲大陸的數學家停止了思想交換。因為牛頓在關於微積分的主要工作和第一部出版物,即《
自然哲學的數學原理》中使用了幾何方法。所以在牛頓死後的一百多年裡,英國人繼續以幾何為主要工具。而大陸的數學家繼續萊布尼茲的分析法,使它發展並得到改善,這些事情的影響非常巨大,它不僅使英國的數學家落後在後面,而且使數學損失了一些最有才能的人套用可作出的貢獻。
第二次危機
微積分誕生之後,數學迎來了一次空前繁榮的時期,對18世紀的數學產生了重要而深遠的影響,但是牛頓和萊布尼茨的微積分都缺乏清晰的、嚴謹的邏輯基礎,這在初創時期是不可避免的。科學上的巨大需要戰勝了邏輯上的顧忌。他們需要做的事情太多了,他們急於去攫取新的成果。基本問題只好先放一放,正如
達朗貝爾所說的:“向前進,你就會產生信心!”
數學史的發展一再證明自由創造總是領先於形式化和邏輯基礎。
於是在微積分的發展過程中,出現了這樣的局面:一方面是微積分創立之後立即在科學技術上獲得套用,從而迅速地發展;另一方面是微積分學的理論在當時是不嚴密的,出現了越來越多的悖論和謬論。數學的發展又遇到了深刻的令人不安的危機。例如,有時把
無窮小量看作不為零的有限量而從等式兩端消去,而有時卻又令無窮小量為零而忽略不計。由於這些矛盾,引起了數學界的極大爭論。如當時愛爾蘭主教、
唯心主義哲學家
貝克萊嘲笑“無窮小量”是“已死的幽靈”。貝克萊對牛頓
導數的定義進行了批判。
當時牛頓對導數的定義為:
當
增長為
時,
的立方(記為
)成為
的立方(記為
),即
的立方結果為
。
與
的增量分別為
和
。
的增量除以
的增量的結果為
,然後代入h=0讓增量消失,則它們的最後結果為
。我們知道這個結果是正確的,但是推導過程確實存在著明顯的偷換假設的錯誤:在論證的前一部分假設
是不為0的,而在論證的後一部分又被取為0。那么
到底是不是0呢?這就是著名的
貝克萊悖論。這種微積分的基礎所引發的危機在數學史上稱為
第二次數學危機,而這次危機的引發與牛頓有直接關係。歷史要求給微積分以嚴格的基礎。
補救
第一個為補救第二次數學危機提出真正有見地的意見的是法國數學家
達朗貝爾。他在1754年指出,必須用更可靠的理論去代替當時使用的粗糙的
極限理論。但是他本人未能提供這樣的理論。最早使微積分嚴格化的是
拉格朗日。為了避免使用無窮小推理和當時還不明確的極限概念,拉格朗日曾試圖把整個微積分建立在
泰勒公式的基礎上。但是,這樣一來,考慮的函式範圍太窄了,而且不用極限概念也無法討論無窮級數的
收斂問題,所以,拉格朗日的以
冪級數為工具的
代數方法也未能解決微積分的奠基問題。
到了19世紀,出現了一批傑出的數學家,他們積極為微積分的奠基工作而努力,其中包括了捷克的哲學家
波爾查諾,他曾著有《無窮的悖論》,明確地提出了級數收斂的概念,並對極限、
連續和變數有了較深入的了解。
分析學的奠基人,法國數學家柯西在1821—1823年間出版的《分析教程》和《無窮小計算講義》是數學史上劃時代的著作。在那裡他給出了
數學分析一系列的基本概念和精確定義。
對分析基礎做更深一步的理解的要求發生在1874年。那時的德國數學家維爾斯特拉斯構造了一個沒有導數的連續函式,即構造了一條沒有切線的連續曲線,這與直觀概念是矛盾的。它使人們認識到極限概念、
連續性、
可微性和收斂性對
實數系的依賴比人們想像的要深奧得多。
黎曼發現,柯西沒有必要把他的
定積分限制於
連續函式。黎曼證明了,被積函式不連續,其定積分也可能存在。也就是將柯西積分改進為
黎曼積分。
這些事實使我們明白,在為分析建立一個完善的基礎方面,還需要再深挖一步:理解實數系更深刻的性質。這項工作最終由維爾斯特拉斯完成,使得數學分析完全由實數系導出,脫離了知覺理解和幾何直觀。這樣一來,數學分析所有的基本概念都可以通過實數和它們的基本運算表述出來。微積分嚴格化的工作終於接近封頂,只有關於無限的概念沒有完全弄清楚,在這個領域,德國數學家
康托爾做出了傑出的貢獻。
總之,第二次數學危機和核心是微積分的基礎不穩固。柯西的貢獻在於,將微積分建立在極限理論的基礎上。維爾斯特拉斯的貢獻在於邏輯地構造了
實數論。為此,建立分析基礎的
邏輯順序是實數系——
極限論——微積分。
18世紀的分析學
驅動18世紀的微積分學不斷向前發展的動力是物理學的需要,物理問題的表達一般都是用微分方程的形式。18世紀被稱為數學史上的英雄世紀。他們把微積分套用於天文學、
力學、光學、
熱學等各個領域,並獲得了豐碩的成果。在數學本身又發展出了多元微分學、多重積分學、微分方程、無窮級數的理論、
變分法,大大地擴展了數學研究的範圍。其中最著名的要數
最速降線問題:即最快下降的曲線的問題。這個曾經的難題用變分法的理論可以輕而易舉的解決。
創立意義
微積分學的創立,極大地推動了數學的發展,過去很多用初等數學無法解決的問題,運用微積分,這些問題往往迎刃而解,顯示出微積分學的非凡威力。
前面已經提到,一門學科的創立並不是某一個人的業績,而是經過多少人的努力後,在積累了大量成果的基礎上,最後由某個人或幾個人總結完成的,微積分也是這樣。
不幸的是,由於人們在欣賞微積分的宏偉功效之餘,在提出誰是這門學科的創立者的時候,竟然引起了一場軒然大波,造成了歐洲大陸的數學家和英國數學家的長期對立。英國數學在一個時期里閉關鎖國,囿於民族偏見,過於拘泥在牛頓的“流數術”中停步不前,因而數學發展落後了整整一百年。
其實,牛頓和萊布尼茨分別是自己獨立研究,在大體上相近的時間裡先後完成的。比較特殊的是牛頓創立微積分要比萊布尼茨早10年左右,但是正式公開發表微積分這一理論,萊布尼茨卻要比牛頓發表早三年。他們的研究各有長處,也都各有短處。那時候,由於民族偏見,關於發明優先權的爭論竟從1699年始延續了一百多年。
應該指出,這是和歷史上任何一項重大理論的完成都要經歷一段時間一樣,牛頓和萊布尼茨的工作也都是很不完善的。他們在無窮和
無窮小量這個問題上,其說不一,十分含糊。牛頓的無窮小量,有時候是零,有時候不是零而是有限的小量;萊布尼茨的也不能自圓其說。這些基礎方面的缺陷,最終導致了
第二次數學危機的產生。
直到19世紀初,法國科學學院的科學家以
柯西為首,對微積分的理論進行了認真研究,建立了
極限理論,後來又經過德國數學家
維爾斯特拉斯進一步的嚴格化,使極限理論成為了微積分的堅定基礎。才使微積分進一步的發展開來。
相關評價
馮·諾依曼:微積分是現代數學的第一個成就,而且怎樣評價它的重要性都不為過。我認為,微積分比其他任何事物都更清楚地表明了現代數學的發端;而且,作為其邏輯發展的數學分析體系仍然構成了精密思維中最偉大的技術進展。
阿蒂亞:人們要求降低微積分學在科學教育中的地位,而代之以與計算機研究關係更密切的
離散數學的呼聲日漸高漲。...許多離散現象的重要結果還是通過使用微積分才得到了最好的證明。直到現在,分析無窮性的微積分學的中心地位仍然是無可爭議的。
在多元微積分學中,
牛頓-萊布尼茨公式的對照物是
德雷克公式、
散度定理、以及經典的
斯托克斯公式。無論在觀念上或者在技術層次上,他們都是牛頓-萊布尼茨公式的推廣。隨著數學本身發展的需要和解決問題的需要,僅僅考慮
歐式空間中的微積分是不夠的。有必要把微積分的演出舞台從歐式空間進一步拓展到一般的
微分流形。在微分流形上,
外微分式扮演著重要的角色。於是,外微分式的積分和微分流形上的斯托克斯公式產生了。而經典的德雷克公式、散度定理、以及經典的斯托克斯公式也得到了統一。
微積分的發展歷史表明了人的認識是從生動的直觀開始,進而達到抽象思維,也就是從感性認識到理性認識的過程。人類對客觀世界的規律性的認識具有相對性,受到時代的局限。隨著人類認識的深入,認識將一步一步地由低級到高級、由不全面到比較全面地發展。人類對自然的探索永遠不會有終點。
套用及發展
從17世紀開始,隨著社會的進步和
生產力的發展,以及如航海、天文、礦山建設等許多課題要解決,數學也開始研究變化著的量,數學進入了“變數數學”時代。整個17世紀有數十位科學家為微積分的創立做了開創性的研究,但使微積分成為數學的一個重要分支的還是
牛頓。
 圖3微積分雜誌
圖3微積分雜誌(1)運動中速度與距離的互求問題
已知物體移動的距離
表為以時間為變數的函式
,求物體在任意時刻的速度和加速度;反過來,已知物體的加速度表為以時間為變數的函式公式,求速度和距離。這類問題是研究運動時直接出現的,困難在於,所研究的速度和加速度是每時每刻都在變化的。比如,計算物體在某時刻的
瞬時速度,就不能像計算平均速度那樣,用移動的距離去除運動的時間,因為在給定的瞬間,物體移動的距離和所用的時間是
,而
是無意義的。但是,根據物理,每個運動的物體在它運動的每一時刻必有速度,這也是無疑的。已知速度公式求移動距離的問題,也遇到同樣的困難。因為速度每時每刻都在變化,所以不能用運動的時間乘任意時刻的速度,來得到物體移動的距離。
(2)求曲線的切線問題
這個問題本身是純幾何的,而且對於科學套用有巨大的重要性。由於研究天文的需要,光學是十七世紀的一門較重要的科學研究,透鏡的設計者要研究光線通過
透鏡的通道,必須知道光線入射透鏡的角度以便套用
反射定律,這裡重要的是光線與曲線的
法線間的夾角,而法線是垂直於
切線的,所以總是就在於求出法線或切線;另一個涉及到曲線的切線的科學問題出現於運動的研究中,求運動物體在它的軌跡上任一點上的運動方向,即軌跡的切線方向。
(3)求長度、面積、體積、與重心問題等
這些問題包括,求曲線的長度(如
行星在已知時期移動的距離),曲線圍成的面積,曲面圍成的體積,物體的重心,一個相當大的物體(如行星)作用於另一物體上的引力。實際上,關於計算橢圓的長度的問題,就難住數學家們,以致有一段時期數學家們對這個問題的進一步工作失敗了,直到下一世紀才得到新的結果。又如求面積問題,早在
古希臘時期人們就用
窮竭法求出了一些面積和體積,如求
拋物線在
區間 上與
軸和直線
所圍成的面積
,他們就採用了窮竭法。當分割的份數越來越多時,所求得的結果就越來越接近所求的面積的精確值。但是,套用窮竭法,必須添上許多技藝,並且缺乏一般性,常常得不到數字解。當
阿基米德的工作在歐洲聞名時,求長度、面積、體積和重心的興趣復活了。窮竭法先是逐漸地被修改,後來由於微積分的創立而根本地修改了。
(4)求
最大值和最小值問題(二次函式,屬於微積分的一類)
例如炮彈在炮筒里射出,它運行的水平距離,即射程,依賴於炮筒對地面的傾斜角,即發射角。一個“實際”的問題是:求能夠射出最大射程的發射角。十七世紀初期,Galileo斷定(在真空中)發射角是
時達到最大射程;他還得出炮彈從各個不同角度發射後所達到的不同的最大高度。研究行星的運動也涉及到最大值和最小值的問題。
近現代發展
人類對自然的認識永遠不會止步,微積分這門學科在現代也一直在發展著。以下列舉了幾個例子,足以說明人類認識微積分的水平在不斷深化。
在黎曼將柯西的積分含義擴展之後,
勒貝格又引進了測度的概念,進一步將黎曼積分的含義擴展。例如著名的
狄利克雷函式在黎曼積分下不可積,而在
勒貝格積分下便可積。
前蘇聯
前蘇聯著名數學大師
舍蓋·索伯列夫為了確定
偏微分方程解的存在性和唯一性,建立了
廣義函式和
廣義導數的概念。這一概念的引入不僅賦予微分方程的解以新的含義,更重要的是,它使得
泛函分析等數學工具得以套用到微分方程理論中,從而開闢了微分方程理論的新天地。
美國
美籍華裔數學大師陳省身所研究的微分幾何領域,便是利用微積分的理論來研究幾何,這門學科對人類認識時間和空間的性質發揮著巨大的作用,並且這門學科至今仍然很活躍。前不久由俄羅斯數學家
佩雷爾曼完成的
龐加萊猜想便屬於這一領域。
中國
中國的數學愛好者發現了
積乘和
微商,使微積分的內容進一步拓展。
計算工具
隨著當今科技的發展,一些計算器也能對微積分(
微分和
定積分)進行求解。以下是能解微積分的函式計算器(以下型號僅供參考):
(1)非編程系列:
fx-100MS、fx-115MS、fx-570MS、fx-991MS系列;
ES系列(自然書寫顯示):
fx-115ES、fx-570ES、fx-991ES系列;
ES PLUS系列(自然書寫顯示):
fx-115ES PLUS、 fx-570ES PLUS、 fx-991ES PLUS、 fx-991ES PLUS C、 fx-991cn x系列。
(2)可程式系列:
fx-3650p、fx-3950p、fx-4800p、fx-5800p、fx-7400G、fx-9750G、fx-9860G以及其升級版本。













 圖1萊布尼茨
圖1萊布尼茨 圖2 牛頓-萊布尼茨公式
圖2 牛頓-萊布尼茨公式










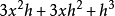





 圖3微積分雜誌
圖3微積分雜誌
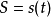


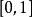

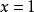
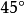














 圖1萊布尼茨
圖1萊布尼茨 圖2 牛頓-萊布尼茨公式
圖2 牛頓-萊布尼茨公式










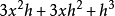
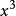





 圖3微積分雜誌
圖3微積分雜誌